MRI Simulation - Sequence
这篇主要是讲 Steady state 的基本计算方式,也没有那么难?
Simple situation
只考虑 repetition. 这里 $TE1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17% ----------假设------------
df = 0; % Hz off-resonance.
T1 = 600; % ms.
T2 = 100; % ms.
TE = 1; % ms.
flip = pi/3; % radians.
M = [0;0;1];
% --------start----------
Rflip = yrot(flip);
[Ate,Bte] = freeprecess(TE,T1,T2,df);
M = Rflip*M; % Magnetization after tip.
M = Ate*M+Bte % Magnetization at TE.
在上面,仅仅是重复了上一章节的 Precession. 接下来,给定 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35df = 0; % Hz off-resonance.
T1 = 600; % ms.
T2 = 100; % ms.
TE = 1; % ms.
dT = 1;
TR = 500; % ms.
flip = pi/3; % radians.
Ntr = round(TR/dT);
Nex = 10; % 10 excitations.
M = [0;0;1];
Rflip = yrot(flip);
[A1,B1] = freeprecess(dT,T1,T2,df);
M(1,Nex*Ntr)=0; % 广播机制:扩充矩阵
Mcount=1;
for n=1:Nex
M(:,Mcount) = Rflip*M(:,Mcount); % 激发:旋转算子作用
for k=1:Ntr
Mcount=Mcount+1;
M(:,Mcount)=A1*M(:,Mcount-1)+B1; % 经过dT时间,M发生一些变化
end;
end;
% --------plot----------
time = [0:Mcount-1]*dT;
plot(time,M(1,:),'b-',time,M(2,:),'r--',time,M(3,:),'g-.');
legend('M_x','M_y','M_z');
xlabel('Time (ms)');
ylabel('Magnetization');
axis([min(time) max(time) -1 1]);
grid on;
这里隐含了一件事:考虑每个时间微元下的变化量的时候,仍然是
制图结果: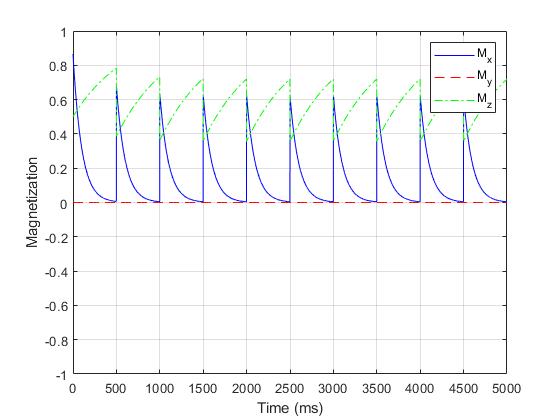
可以看到,从某一个 excitation 开始,图线就成了一个周期函数(每个周期的图线相差的不是很大了)。这样的周期我们就称之为steady state. 那么这个时候,我们可以认为:M 经激发以及 $TR$ 时间的 relaxation之后,又会回到原来的状态。也就是:M1 = Atr*Rflip*M+Btr = M. 于是就能通过一行代码解出 steady state 下的 M 应该是多大:1
Mss = inv(eye(3)-Atr*Rflip)*Btr
下面都记 steady state 下的 magnetization 为 $M{ss}$。
在此基础上,计算在任意 $TE
= tip 之前的M = tip 之后的M = tip 之后经 时间的M
他们很显然满足以下关系:
- M2 = Rflip * M1
- M3 = Ate * M2 + Bte
- M1 = Atr * M3 + Btr
其中te表示 tip 之后经 tr表示在同一周期内经 M3 = Ate*Rflip*Atr*M3 + (Ate*Rflip*Btr+Bte)
一行代码解决:1
inv(eye(3)-Ate*Rflip*Atr) * (Ate*Rflip*Btr+Bte)