MRI Simulation - Precession

这是一些关于 MRI 实际模拟及遇到的问题的过程记录。

准备

理论基础在 Liang 或者 Nishimura 的书上已经写得很清楚了，这里不再重复他们的理论推导。

首先假定 。这里 表示 eqilibrium nuclear magnetization， 它是一个标量。

Relaxation

这里假设 T1, T2 是同时考虑的，那么经过 T1, T2 relaxation 之后的 M 应为

$$M \leftarrow \begin{bmatrix} e^{-t / T_2} & 0 &0 \\ 0 & e^{-t / T_2} 0&0 \\ 0& 0& e^{-t / T_1} \end{bmatrix}M + \begin{bmatrix} 0\\ 0\\ M_0\left ( 1- e^{-t / T_1} \right ) \end{bmatrix}$$

Rotation

定义 为矢量 M 关于 z轴逆时针旋转了角度。其相当于对矢量 M 左乘了如下矩阵：

$$R_z\left ( \phi \right ) = \begin{bmatrix} \cos\phi & -\sin\phi &0 \\ \sin\phi & \cos\phi &0 \\ 0&0 &1 \end{bmatrix}, M \leftarrow R_z\left ( \phi \right )M$$

类似定义关于x, y轴的旋转乘子：

$$R_x\left ( \phi \right ) = \begin{bmatrix} 1 & 0 &0 \\ 0 & \cos\phi &-\sin\phi \\ 0 & \sin\phi &\cos\phi \end{bmatrix}$$ $$R_y\left ( \phi \right ) = \begin{bmatrix} \cos\phi & 0 &\sin\phi \\ 0 & 1 &0 \\ -\sin\phi & 0 &\cos\phi \end{bmatrix}$$

注意这里的旋转方向，与 Nishimura 书上规定的方向是不同的。这里的旋转方向是 right-handed rule。比如绕Z轴旋转45°，则表示将右手大拇指指向Z轴正方向时，手指蜷起来的方向。 Nishimura 书上的 rotation matrices 为 left-handed rule, 其矩阵为这里的矩阵的转置。

作为例子，在这里展示 的代码，其余代码类似。

function Rz = zrot(phi)
Rz = [cos(phi) -sin(phi) 0; sin(phi) cos(phi) 0; 0 0 1];

若规定按任意角度(transverse axis other than x or y)为轴进行旋转，设定旋转矩阵为 ，其中 定义不变，表示该轴与 y 轴的夹角，则：

$$R_{th}\left ( \phi , \theta \right ) = R_z\left ( \theta \right )*R_x\left ( \phi \right )*R_z\left ( - \theta \right )$$

并遵循矩阵乘法规则，从最右边一个矩阵开始作用于 M。

function Rth=throt(phi, theta)
Rz = zrot(-theta);
Rx = xrot(phi);
Rth = inv(Rz) * Rx * Rz;

Free Precession with Relaxation

T1, T2 定义类似. df = off-resonance frequency 。
这里是假定 homoegeneous 情况下的，所以没有 .

function [Afp, Bfp] = freeprecess(T,T1,T2,df)
phi = 2*pi*df*T/1000;	% Resonant precession, radians.
E1 = exp(-T/T1);	
E2 = exp(-T/T2);

Afp = [E2 0 0;0 E2 0;0 0 E1]*zrot(phi);
Bfp = [0 0 1-E1]';

按照以下代码进行数据可视化。dT表示采样时间。

dT = 1;		% 1ms delta-time.
T = 1000;	% total duration
N = ceil(T/dT)+1; % number of time steps.
df = 10;	% Hz off-resonance.
T1 = 600;	% ms.
T2 = 100;	% ms.

% ===== Get the Propagation Matrix ======

[A,B] = freeprecess(dT,T1,T2,df);


% ===== Simulate the Decay ======

M = zeros(3,N);	% Keep track of magnetization at all time points.
M(:,1)=[1;0;0];	% Starting magnetization.

for k=2:N
	M(:,k) = A*M(:,k-1)+B;
end;


% ===== Plot the Results ======

time = [0:N-1]*dT;
plot(time,M(1,:),'b-',time,M(2,:),'r--',time,M(3,:),'g-.');
legend('M_x','M_y','M_z');
xlabel('Time (ms)');
ylabel('Magnetization');
axis([min(time) max(time) -1 1]);
grid on;

就可以得到 $M{x}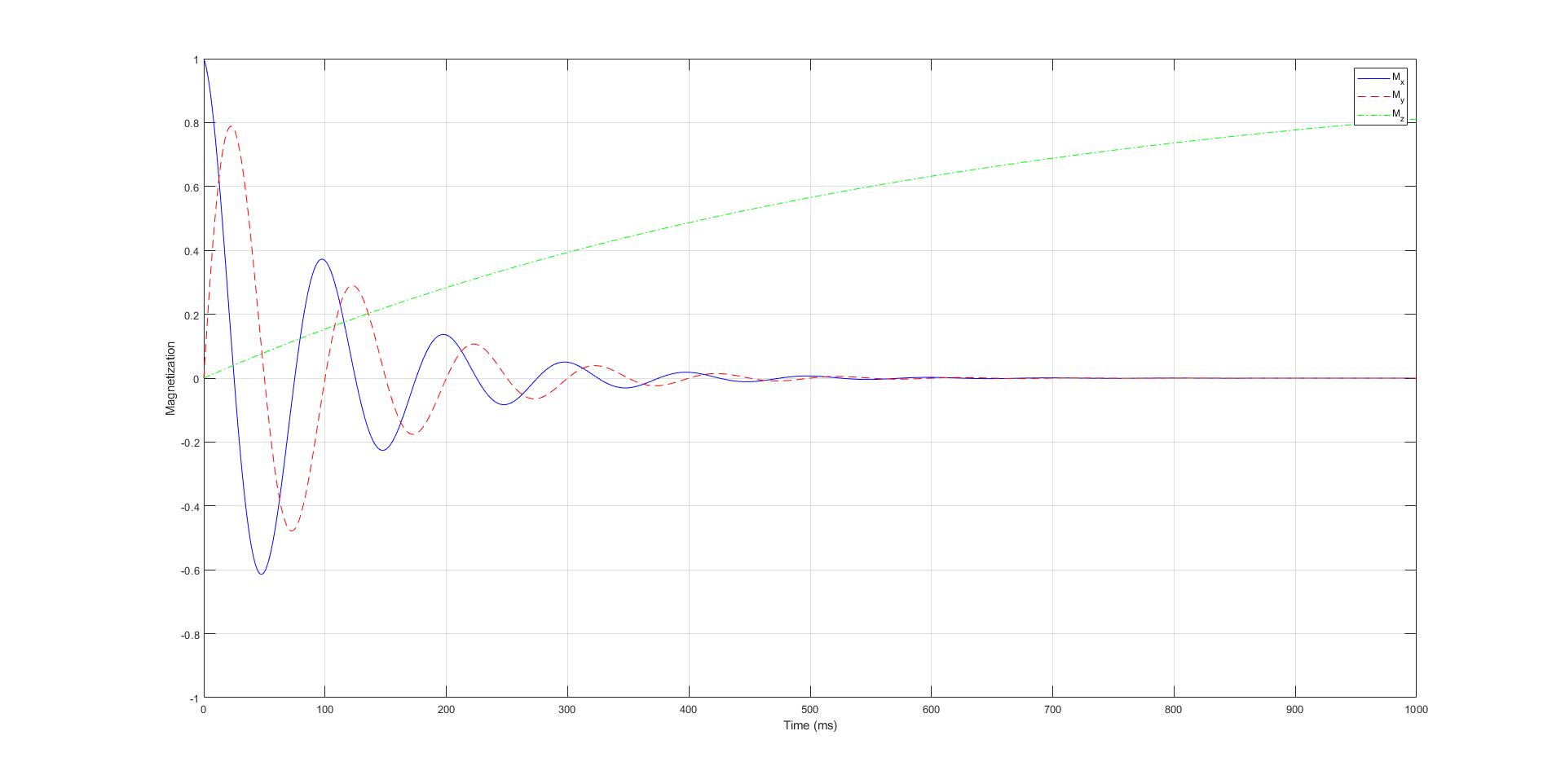M{y}M_{z}$ 的变化曲线：

不是很清楚，但还能凑合看看。